|
1 引 言 TOFD 超聲波衍射時間差(time-of-flight-diffrac-tion, TOFD)測量技術[1]是一種可以精確定量的檢測技術,該方法通過測量缺陷邊緣的衍射超聲波信號之間傳播的時間差,對缺陷的位置和大小進行測量。該技術 融合了超聲波檢測和射線檢測的優點,能夠對缺陷準確地定性和定量。在發達國家,TOFD檢測技術近年來已被廣泛應用于中厚板對接焊縫的檢測與缺陷定量中, 國內也在積極推進 TOFD 方法代替射線檢測的標準。TOFD 法依賴于超聲波與缺陷端部的相互作用而在較大角度范圍內發射的衍射波,檢出衍射波就能確定缺陷的存在,而信號傳播的時間差就是缺陷高度量值。缺陷尺寸根據 衍射信號傳播的時間而非幅度來測量。因此,對端部衍射信號的時間差測量就成為TOFD缺陷定量的關鍵。但是超聲信號容易受到材料的結構噪聲以及儀器電噪聲 等噪聲影響,且由于 TOFD 技術檢測的是相對微弱且指向性差的衍射波信號,導致端點衍射回波容易被雜波所淹沒或者波幅太低難以識別,使信號的時間差測量誤差增大,從而使缺陷定量時的 誤差相應增大。因此,采用有效的信號處理方法來抑制噪聲信號[2],提高衍射回波信號的信噪比對缺陷定量以及 TOFD 成像就顯得尤為重要。 目前,處理超聲回波信號的方法有互相關法和小波變換法。當信號噪聲為高斯白噪聲,接收信號與參考信號一致時,互相關法比較適合[3,4]。小波 變換在處理超聲信號時用得比較廣泛,但是,在低頻信號時,它的時間測量精度低;在高頻信號時,它的頻率測量精度低。本文在分離譜技術的基礎上采用最小值被 選中次數加權算法去除TOFD檢測信號中的結構噪聲,與傳統的帶通濾波法相比,可以有效提高 TOFD 的定量精度。 2 分離譜技術的算法原理 超聲檢測信號中電噪聲的幅度和相位均是隨機的,而且各次測量所得的結果互不相關,采用基于時間平均的同步疊加法可以使干擾信號在很大程度上正負 抵消。結構噪聲是材料中的晶界及組織不均勻對超聲波的散射作用而引起的散射回波,它是與特定頻率有關的相干噪聲,當頻率不同時,其幅度、相位等均有顯著的 變化。 分離譜法[5,6]就是利用結構噪聲和目標回波對頻率變化敏感性上的差異而建立起來的解相關方法。當超聲波頻率變化時,材料結構引起的結構噪聲回波幅度將 發生較大的變化,而缺陷回波的幅度變化將相對較少。因此,若對 TOFD 探頭發射的寬聲束超聲波信號進行譜分離,那么在不同頻譜段的結構噪聲回波信號幅度會有明顯的不同,而缺陷回波的變化幅度則相對穩定,這樣就可以利用分離譜 技術來提高 TOFD 衍射信號的信噪比。分離譜算法的具體實現過程如圖 1 所示。 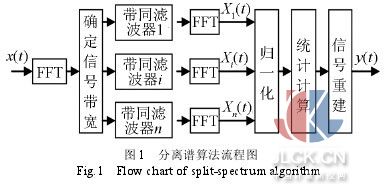
首先將接收到的數字化超聲信號作快速傅立葉變換,得到信號的全頻譜,并在一定的信號頻帶內設置若干不同中心頻率、等帶寬的窄帶濾波器,超聲信號 通過這些窄帶濾波器后將得到一系列中心頻率不同的窄帶信號,這個過程稱為信號分離;再以分離后的不同中心頻率的窄帶信號為變量進行統計運算,從而得到經過 非線性濾波處理的輸出信號,也即信號的重建。 在信號分離階段,高斯形帶通濾波器比較適合處理服從正態分布的信號,并且其時頻特性均比較理想;信號恢復階段是整個分離譜技術的關鍵所在,它是 指對所有的分離信號引人非線性相關運算,以達到降低噪聲、提高信噪比的目的。目前常用的恢復算法有最小值算法、極性閾值法、線性平均法和最小值加極性閾值 算法幾種[6]。文獻[7]證實,以上算法中最小值算法對于提高信號的信噪比具有明顯的作用,但它的缺點是對濾波器數目比較敏感,導致此算法不夠穩定。 本文采用等帶寬高斯型窄帶通濾波器構成的濾波器組對原始信號進行分離,信號恢復是在最小值算法的基礎上,采用分離信號被選中次數的加權恢復算法 [8]進行信號恢復。該方法本質上類似于維納濾波器的傳遞函數,無需信號和噪聲頻譜的先驗知識,對濾波器的數目也不敏感,從而能自適應地處理寬帶的目標反 射脈沖波,達到濾波精度的要求。最小值被選中次數加權恢復算法的原理[8]為: 首先將檢測到的信號做傅立葉變換得到信號的幅度譜,并在一定的幅度能量頻帶內設置若干不同中心頻率的窄帶濾波器,假定這些濾波器的數目為 N個,待處理的數字信號含有M 個采樣點,采樣周期為sT ,則數據的長度為 ( 1)sM T,可以從 N 個帶通濾波器輸出端得到 N 個備選的窄帶信號xiti =1,2, , N,每個窄帶信號都有各自特定的中心頻率。最小值法的原理就是在 M 個采樣點分別對 N 個窄帶信號 ( )ix t 求最小值,并以此最小值作為各瞬時點的信號輸出,此時輸出為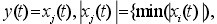 i =1 ,2,N}(符號與原符號相同),也就是說,需要在M 個采樣點處進行 M 次選最小值的運算。如果單個窄帶信號被選中的次數為im ,則總選中次數為: i =1 ,2,N}(符號與原符號相同),也就是說,需要在M 個采樣點處進行 M 次選最小值的運算。如果單個窄帶信號被選中的次數為im ,則總選中次數為: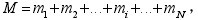 ,由此可定義各窄帶信號ix 的權值 ,由此可定義各窄帶信號ix 的權值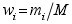 。在統計意義上,高信噪比頻帶信號被選中的次數是最多的,因而,在較大的im 處,該頻帶信號xi t 所對應的中心頻率處將有一個較高的峰值。如果我們根據信噪比對信號進行加權,對具有較高信噪比的分離信號賦予較高的權值iw ,也即重建后的信號 。在統計意義上,高信噪比頻帶信號被選中的次數是最多的,因而,在較大的im 處,該頻帶信號xi t 所對應的中心頻率處將有一個較高的峰值。如果我們根據信噪比對信號進行加權,對具有較高信噪比的分離信號賦予較高的權值iw ,也即重建后的信號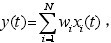 ,那么按此方法恢復出來的信號必然能夠達到較高的信噪比。 ,那么按此方法恢復出來的信號必然能夠達到較高的信噪比。 3 實驗結果及分析 按照 TOFD 檢測標準,實驗所用試塊為 150mm×200mm×30mm(長×寬×高)的鋼樣塊,試塊的側面從上到下分別打上直徑為 3、 3、 2毫米的橫穿孔,見圖 2。采用美國聲學物理公司的 IPR1210發射接收卡,射頻輸出口接到工控機上的 PCI8002數據采集卡。采集卡的采樣頻率為 40MHz。探頭選用標稱角度為 60°,中心頻率選擇為 5MHz,晶片直徑為 6mm 的 TOFD 探頭。探頭分置于試塊模擬缺陷的兩邊,使模擬缺陷剛好位于兩探頭的中間,探頭間距為 S=1.73d,其中 d=22mm 為最大埋深,即缺陷軸線高度離板材表面距離。實驗采集到的原始信號及分離譜算法處理后的結果如圖 3。 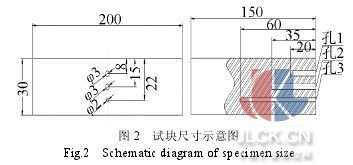
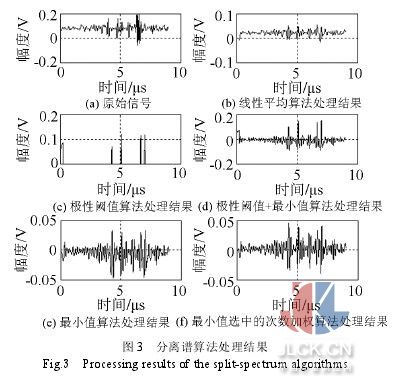
從圖 3(a)的原始信號波形可以看到,受噪聲的影響,原始信號的信噪比是比較低的,各目標回波的波形也無法分清,影響了 TOFD 法的定位和定量。下面采用分離譜算法對原始信號進行處理。 根據分離譜算法的原理,實驗采用 N=15 個等帶寬的高斯窄帶通濾波器組成的濾波器組對預處理后的信號進行分離(起始濾波器中心頻率為0.9MHz;相鄰濾波器中心頻率間隔為 0.4MHz;濾波器帶寬為 0.8MHz),濾波器帶寬為相鄰濾波器中心頻率間隔的 2 倍,窄帶濾波器所覆蓋的處理頻閾寬度為信號頻譜的 3dB 帶寬,由此得到中心頻率各不相同的 15 組窄帶信號。在信號恢復階段采用線性平均、極性閾值、極性閾值+最小值、最小值等四種恢復算法進行信號的重建,所得結果分別如圖3(b)~3(e)所示, 線性平均算法的處理效果最差,而極性閾值算法和最小值+極性閾值算法雖然濾波效果很明顯,但信號的失真現象比較嚴重,最小值算法既滿足了信號增強的要求, 又能減少信號的失真。但最小值算法的最大缺點是對濾波器的數目比較敏感,不同的濾波器數目將產生差別較大的處理結果,這個缺點使得最小值恢復算法的應用受 到很大的限制。而本文采用的最小值選中次數加權恢復算法(結果如圖 3(f)所示)與最小值算法對信號的處理效果相差不大,甚至本文的算法對信號的增強效果更為明顯。而且最小值選中次數加權算法無需信號和噪聲頻譜的先驗知 識,對濾波器的數目也不敏感,具有一定的自適應能力,從而很好地彌補了最小值算法的缺陷。 另外,與傳統的帶通濾波法相比,基于分離譜技術的最小值選中次數加權算法能夠有效地減少結構噪聲對衍射回波的干擾,使缺陷端部衍射回波能夠被準 確識別,減少了時間測量的不確定性對定位和定量精度的影響,從而保證了 TOFD 法中缺陷定位和定量的準確性。假定反射波的中心頻率沒有發生漂移,與發射波的中心頻率相同,則可以用一個中心頻率為5MHz的帶通濾波器對反射波進行濾 波,其通頻帶寬通常取 2MHz。濾波后的波形與最小值選中次數加權算法處理后波形比較如圖 4。 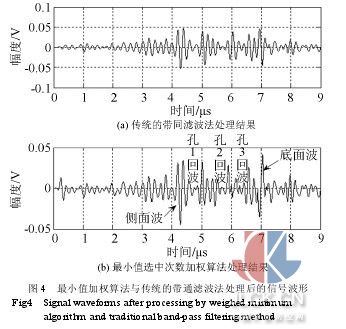
從圖 4(a)中可以看出,由于材料對超聲高頻部分的衰減使反射波的中心頻率比發射波的中心頻率更小,而且原始信號能量最大的頻帶并不是信噪比最高的頻帶,導致 濾波效果較差,無法準確識別出目標回波,影響了缺陷定量的精度。而經過最小值選中次數加權算法處理后的信號(見圖 4(b)),各目標回波的波形清晰,時間關系明顯,減少了時間測量不確定性對測量精度的影響。為了說明這一點,根據公式: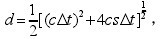 式中: 式中:
c -縱波在材料中的聲速(實測為 5765m/s) t -孔的端部衍射波與側向波的時差 s -兩探頭入射點間距的一半 d -孔的埋藏深度(與板面的距離) 將各參數代入后計算兩種方法處理后的檢測結果,如表 1 所示。 
由表 1 可知,基于分離譜技術的最小值選中次數加權算法相比與傳統的帶通濾波法而言,不僅可以大大地提高信號的信噪比,而且可以增強缺陷定量的準確性,減小了測量的誤差。 4 結 論 TOFD 技術是一種可以精確測量缺陷埋深和自身高度的超聲檢測技術,為評價被檢測件的可靠性提供試驗數據,而信號處理的目的就是為了減小噪聲對目標回波的干擾,使目標回波的波形更加清晰,以提高 TOFD 定量的精度。 本文針對結構噪聲的特點,采用分離譜技術對TOFD 檢測信號進行譜分離,在信號恢復階段采用線性平均等四種恢復算法進行信號的重建,結果表明,以最小值恢復算法的處理效果最好,但最小值算法的最大缺點是對 濾波器的數目比較敏感,導致該算法不夠穩定,因此本文在最小值算法的基礎上引入了最小值選中次數加權算法,得到以下結論: (1) 采用分離譜技術對 TOFD 檢測信號進行譜分離可以提高檢測信號的信噪比; (2) 分離譜分離 TOFD 信號后的不同恢復算法對信噪比影響較大; (3) 基于最小值算法的最小值選中次數加權算法,能夠有效地去除材料的結構噪聲,大大地提高了信號的信噪比。 (4) 采用合適的信號處理方法可以提高 TOFD定量的精度。 本文為超聲TOFD檢測信號的處理提供了一種有益的嘗試,并取得了不錯的實際效果。 摘自:中國計量測控網
|